Activation Functions

Activation Functions are mathematical functions used in Neural Networks (NNs) to introduce non-linearity to the model.

They determine whether a neuron should ve activated or not by transforming input signal into an output signal often between a certain range based on the activation function chosen.

Importance of Activation Functions

• Non-Linearity: Enabling the network to learn more complex patterns and relationships
• Information Flow: Controls the strength and direction of the signal passed on to next layer
• Efficient Training: Helps in convergence during backpropogation by defining useful gradients.

Common Activation Functions

Sigmoid

• Output Range: (0,1)
• Non-linear and differentiable
• Smooth but causes vanishing gradient
• Pros:
  • Interpretable as probability
  • Used for binary classification
• Cons:
  • Vanishing gradient problem for very small or very large inputs
  • Not zero-centered
• Some use cases:
  • Logistic Regression
  • MLP
• 
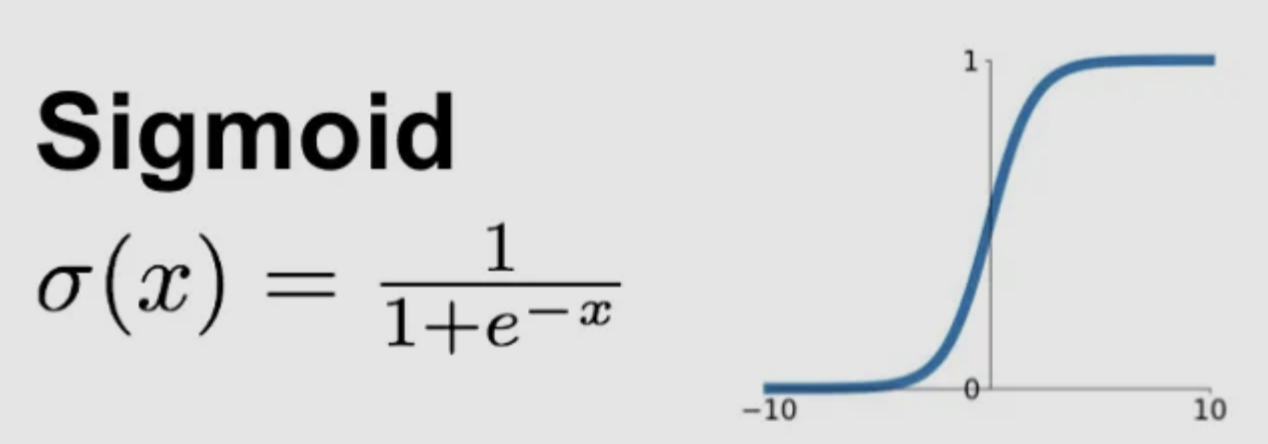
• Basic python implementation:

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.linspace(-10, 10, 100)
y = sigmoid(x)

plt.plot(x, y)
plt.title("Sigmoid Activation")
plt.grid(True)
plt.show()

Tanh

• Output Range: [-1,1]
• Pros:
  • Zero-centered so helps in faster convergence than sigmoid
  • Stronger gradient than sigmoid
• Cons:
  • Also suffers from vanishing gradient for extreme values
• Some use cases:
  • RNNs
  • Older Deep Nets
• 
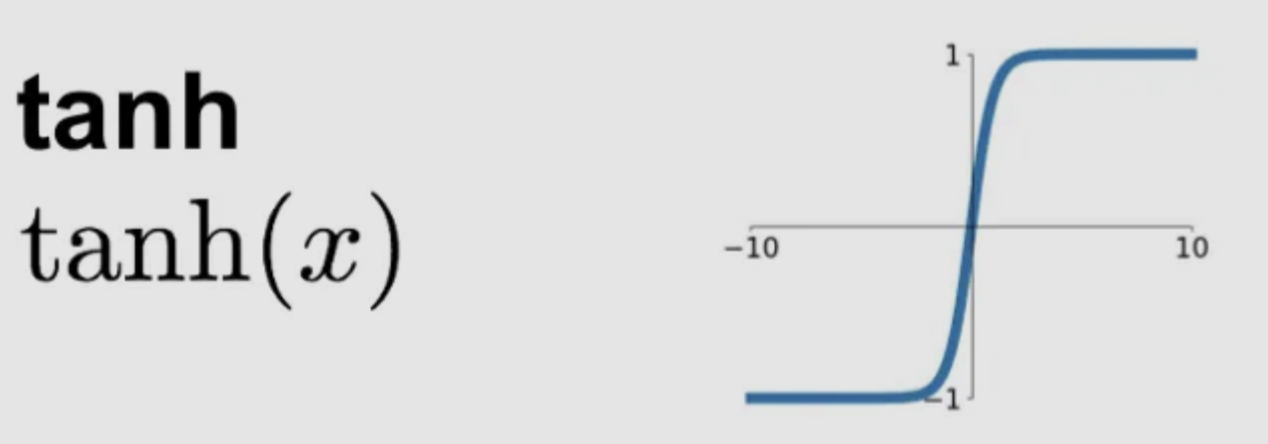
• Basic python implementation:

def tanh(x):
    return np.tanh(x)

y = tanh(x)

plt.plot(x, y)
plt.title("Tanh Activation")
plt.grid(True)
plt.show()

ReLU (Rectified Linera Unit)

• Output Range: (0,INF]
• Non-linear, piecewise linear
• Simple to compute
• Pros:
  • Efficient and fast
  • Sparse activation → only some neurons fire (helps generalization)
  • Doesn’t saturate for positive values
• Cons:
  • Dying ReLU problem: neurons can get stuck during training (output 0 for all inputs)
• Some use cases:
  • CNNs
  • Modern Deep Nets
• 
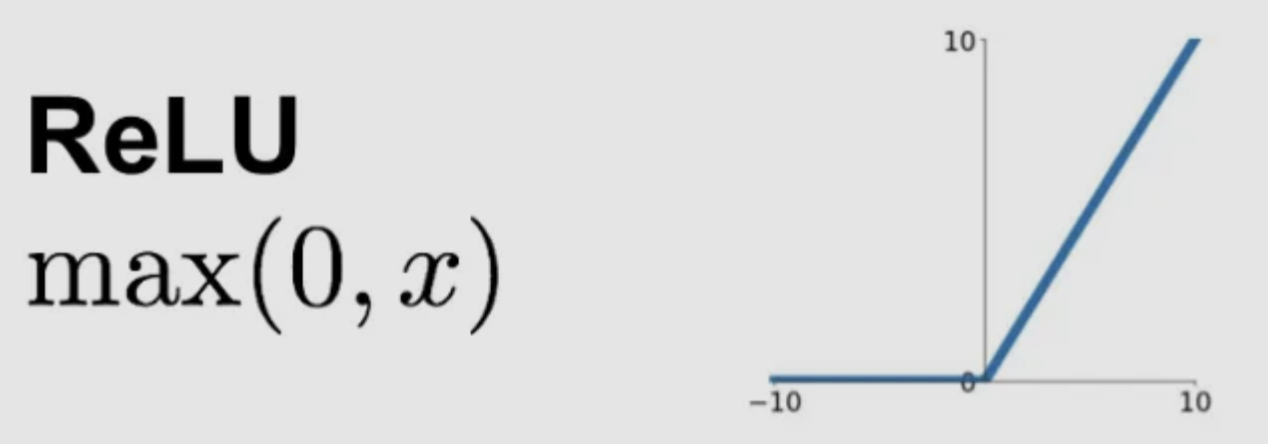
• Basic python implementation:

def relu(x):
    return np.maximum(0, x)

y = relu(x)

plt.plot(x, y)
plt.title("ReLU Activation")
plt.grid(True)
plt.show()

Leaky ReLU

• Output Range: (-INF , INF)
• Fixes ReLU's dying neurons issue
• Allows small negative slope
• Pros:
  • Fixes ReLU’s dying neuron issue
  • Better learning for inputs around zero
• Cons:
  • Still not zero-centered
  • α is a hyperparameter
• Some use cases:
  • Deeper networks where ReLU struggles
  • Hidden layers in GANs and CNNs
• 
• Basic python implementation:

def leaky_relu(x, alpha=0.01):
    return np.where(x > 0, x, alpha * x)

y = leaky_relu(x)

plt.plot(x, y)
plt.title("Leaky ReLU Activation")
plt.grid(True)
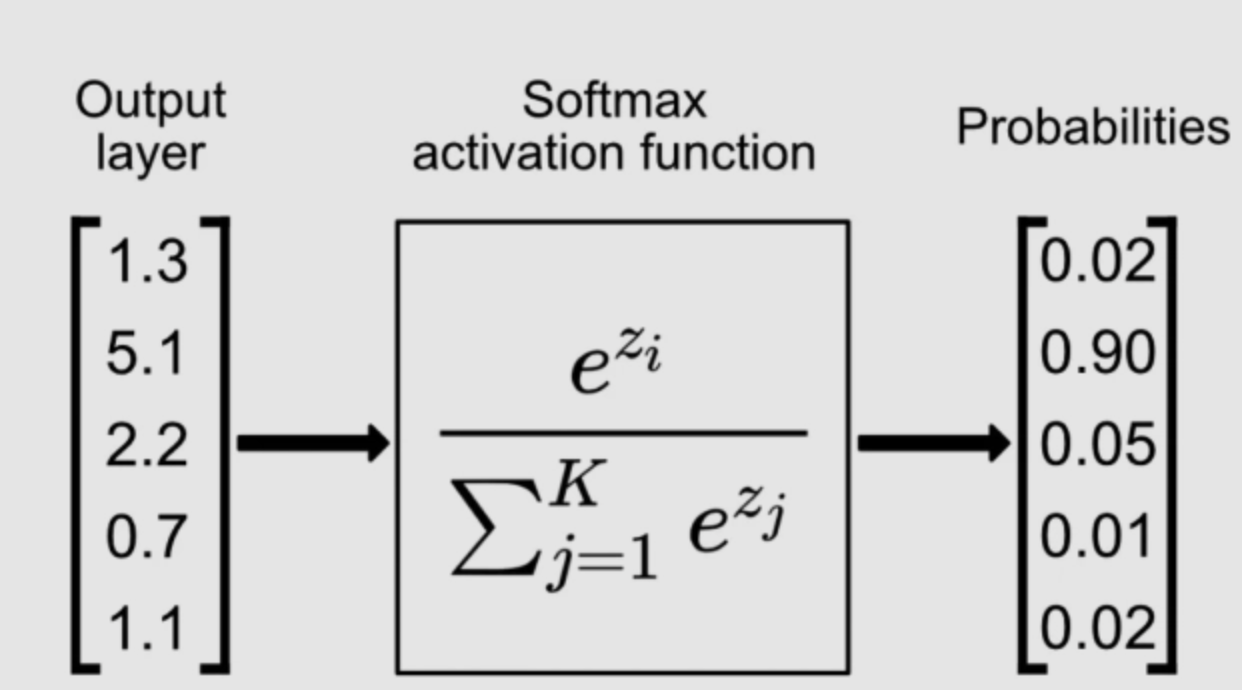
plt.show()

Softmax

• Output Range: (0,1), sums up to 1
• Converts logits to probabilities
• Pros:
  • Great for multi-class classification
  • Probabilistic interpretation
• Cons:
  • Not ideal for hidden layers
  • Sensitive to large input values (can cause numerical instability)
• Some use cases:
  • Output layer in multi-class classification
  • Common in final layers of classification CNNs and RNNs
• 
• Basic python implementation:

def softmax(x):
    e_x = np.exp(x - np.max(x))  # for numerical stability
    return e_x / e_x.sum()

vec = np.array([2.0, 1.0, 0.1])
print("Softmax output:", softmax(vec))

Swish

• Output Range: (-0.28, INF)
• Smooth, non-monotonic
• Combines advantages of linear and sigmoid
• Pros:
  • Performs better than ReLU in deeper networks
  • Avoids dying neuron problem
  • Has a self-gating property
• Cons:
  • More computationally intensive than ReLU
  • Less interpretable
• Some use cases:
  • Deep learning tasks with very deep networks (e.g. NLP, image recognition)
  • Used in models like EfficientNet
• 
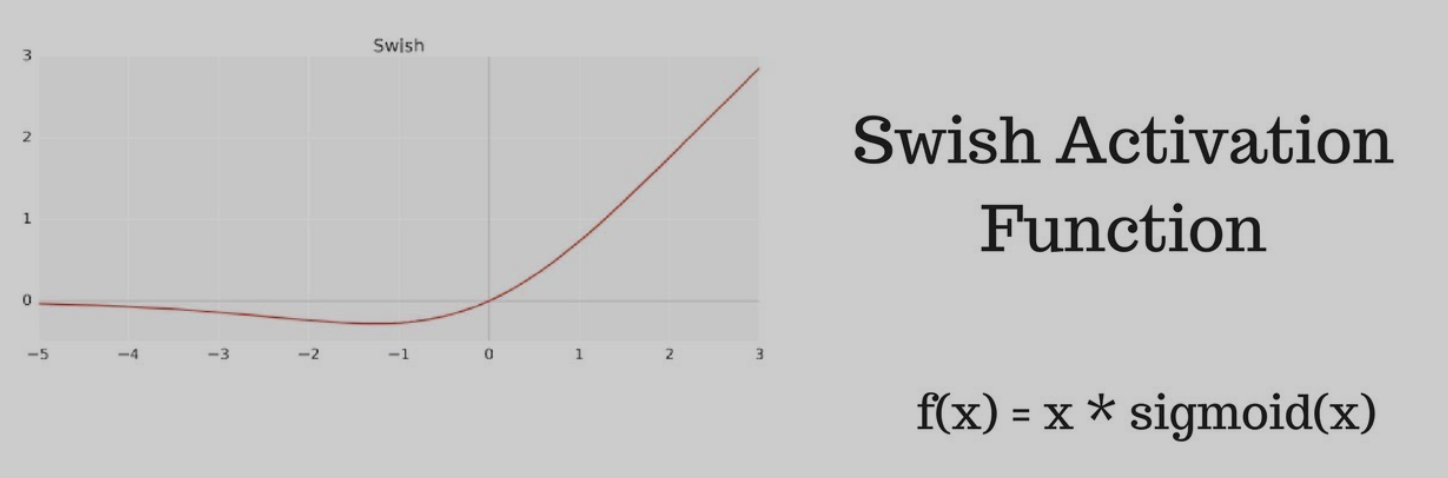
• Basic python implementation:

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def swish(x):
    return x * sigmoid(x)

y = swish(x)

plt.plot(x, y)
plt.title("Swish Activation")
plt.grid(True)
plt.show()

Where Are They Used?

• Hidden layers: Typically use ReLU, Tanh, or Leaky ReLU.
• Output layer:
  • Sigmoid for binary classification.
  • Softmax for multi-class classification.
  • No activation (linear) for regression tasks.